2022寒假集训总结

发表于 更新于 分类于 阅读次数： 本文字数： 3.3k 阅读时长 ≈ 7 分钟

一些知识点的总结以及掌握情况

点双、边双

tarjan

基本能熟练运用\color{blue}\scriptsize\text{基本能熟练运用}

圆方树

对每个点双新建一个“方点”，将内部所有点向“方点”连边。

这样可以形成一棵树。
概念掌握了，但没有做过题。\color{blue}\scriptsize\text{概念掌握了，但没有做过题。}

字符串

kmp & AC 自动机

基本能熟练运用\color{blue}\scriptsize\text{基本能熟练运用}

后缀数组(SA)

将字符串的后缀集合按字典序排序，就可以得到一个后缀数组。

  • rk[i]rk[i]： 从 ii 开始的后缀在后缀数组中的排名。

  • sa[i]sa[i]： 排名为 ii 的后缀的首字母的位置。

    rk[sa[i]]]=sa[rk[i]]=irk[sa[i]]] = sa[rk[i]] = i

  • height[i]height[i]： 排名为 ii 的后缀与排名为 i−1i - 1 的后缀的最长公共前缀(LCP)长度。

    求两个后缀的 LCP ，也就是这两个后缀在后缀数组中区间 heightheight 最小值，常用 st表 维护。

在求后缀数组时，一般使用倍增算法

在第 ii 轮，我们只考虑从每个位置开始长度为 2i2^i 的后缀，这样每次排序就只需要排一个二元组，将两段长度为 2i−12^{i-1} 的子串拼起来，可以利用桶排

总复杂度 O(nlog⁡n)O(n\log n)

具体而言，先按照第二关键字排序，再逆序入桶排第一关键字。

后缀自动机(SAM)

可以识别给定串 SS 的所有后缀的最小 DFA。

  • endpos(s)endpos(s)：原串中所有 ss 出现的结束位置。

    等价关系 endpos(s)=endpos(t)endpos(s)=endpos(t) 会将所有子串划分为若干等价类，这些等价类就是 SAM 中的节点（状态）。

    对于每个等价类，其中子串长度是连续的（某个子串的一段后缀）。

  • parentparent 树：将等价类状态的包含关系视作一棵树。

    par[i]par[i]：ii 在 parentparent 树上的父亲。

  • len[i]len[i]：在 parentparent 树上 ii 所对应的等价类中长度最长的子串。

SAM 在线构建方法

记录当前字符串对应的状态 lstlst，对于新的字符 cc，新建节点 npnp，在 parentparent 树上向上跳到 pp，pp 有 cc 的转移 qq。

如果到根了，par[np]=qpar[np]=q。

否则，需要分类讨论一下，若 len[q]≠len[p]+1len[q] \neq len[p]+1，说明 qq 已经过时了，也就是 endpos(np)≠endpos(q)endpos(np)\neq endpos(q) 此时需要新建一个节点 nqnq，使 len[nq]=len[p]+1len[nq]=len[p]+1，然后将 par[np]=par[q]=nqpar[np]=par[q]=nq。否则，可以直接更新 par[p]par[p]。

构建 SAM 的复杂度是 O(n)O(n) 的
SA 和 SAM 都只会做一些比较板子的题\color{blue}\scriptsize\text{SA 和 SAM 都只会做一些比较板子的题}

Burnside & Pólya

置换群 - OI Wiki
不会（\color{blue}\scriptsize\text{不会（}

树分治

点分治

每次找到树的重心，处理经过重心的路径，然后把重心删除后，在子树中递归处理。

分治过程是 O(nlog⁡n)O(n\log n) 级别的。
基本能独立写完，但是一些细节可能调不出来\color{blue}\scriptsize\text{基本能独立写完，但是一些细节可能调不出来}

边分治

与点分治差不多，每次删除一条边，然后递归处理。

但是对复杂度有一定影响，例如在菊花图时这样做会退化成 O(n2)O(n^2)

因此需要先对树进行三度化，一种比较简单的方法是：左孩子右兄弟。

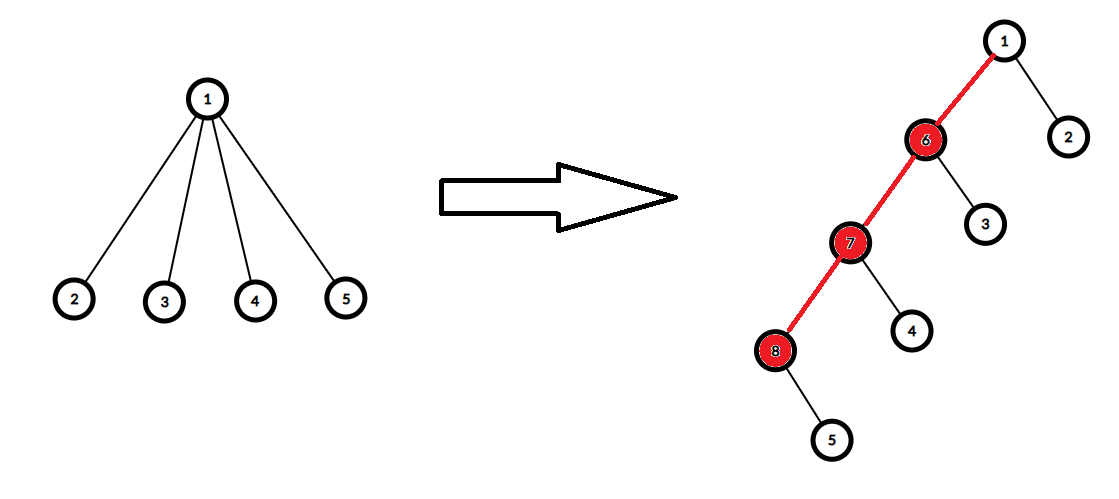
上图中红色部分为新加的用来实现三度化（这个图好像画反了 QAQ，不过不影响理解）
概念理解了，但是没写过\color{blue}\scriptsize\text{概念理解了，但是没写过}

动态点分治

核心是点分树，从重心向子树的重心连边，深度是 O(log⁡n)O(\log n) 级别的。

一般来说会记录子树到根的信息以及子树到根的父亲的信息（用来去掉同一棵子树内的贡献），修改或查询时从当前点跳到根复杂度可以保证。
只会写比较板子的题，不好调\color{blue}\scriptsize\text{只会写比较板子的题，不好调}

LCT 本质是一个 splay 森林，每个 splay 维护原树的一条链，其中序遍历是这条链由浅至深的顺序。

可以动态维护树上的很多东西。
基本能独立写完\color{blue}\scriptsize\text{基本能独立写完}

网络流

Dinic 算法

每次增广前，用 bfs 将图分层，分层后：

  1. 如果不存在源点到汇点的增广路，即可停止增广。
  2. 每次找比当前点层数多 1 的点进行增广（这样可以确保找到的增广路是最短的）

优化：多路增广，当前弧优化

复杂度：O(n2m)O(n^2m)

最大流

找到所有增广路求流量的和。

最小割

等于最大流。

费用流

将 bfs 分层改为用 spfa 跑出最短路图，然后在图上增广。
板子会写，但是一些题建图还不太行\color{blue}\scriptsize\text{板子会写，但是一些题建图还不太行}

决策单调性

斜率优化

将 dp 转移式子写成斜率的形式，通过维护凸包来进行转移。
掌握的还可以\color{blue}\scriptsize\text{掌握的还可以}

四边形不等式优化

若 ww 满足四边形不等式，且区间包含关系单调，则 ff 也满足四 边形不等式。

若 ww 满足四边形不等式，当且仅当

w[i,j]+w[i+1,j+1]≤w[i+1,j]+w[i,j+1]w[i,j]+w[i+1,j+1]\le w[i+1,j]+w[i,j+1]

若 ff 满足四边形不等式，则

p[i,j−1]≤p[i,j]≤p[i+1,j]p[i,j-1]\le p[i,j]\le p[i+1,j]

其中 p[i,j]p[i,j] 为 f[i,j]f[i,j] 的决策点。
代码比较好写，但是不太好发现四边形不等式\color{blue}\scriptsize\text{代码比较好写，但是不太好发现四边形不等式}

一般决策单调性

  • 单调队列/单调栈+二分
    写过一道，掌握的不太好\color{blue}\scriptsize\text{写过一道，掌握的不太好}

  • 分治
    能写完，但一些细节可能调不出来\color{blue}\scriptsize\text{能写完，但一些细节可能调不出来}

  • wqs二分/dp凸优化
    能写出来，但不太好调\color{blue}\scriptsize\text{能写出来，但不太好调}